The best models of how our world works are incomplete. Though they accurately describe much of what Mother Nature has thrown at us, models represent just the tip of the full iceberg and a deeper understanding awaits the endeavoring scientist. Peeling back the layers of the natural world is how we physicists seek a deeper understanding of the universe. This search pushes existing technology to its limits and fuels the innovation seen in modern day nuclear and particle physics experiments.

Today, many of these experiments search for new physics beyond the Standard Model, the theory physicists have accepted to describe the behavior of particles. Some physical phenomena have proven difficult to reconcile with the Standard Model and research seeks to improve understanding of those conundrums, particularly regarding the properties of elusive particles known as neutrinos which have very little mass and no electric charge, and dark matter, a mysterious cosmic ingredient that holds the galaxies together but whose form is not known. The experiments pursuing these phenomena each take a different approach toward these same unknowns resulting in an impressive diversity of techniques geared towards the same goal.
On one side of the experimental spectrum, the Large Hadron Collider smashes together high-energy protons at a rate of one billion collisions per second. These collisions could have the potential to create dark matter particles or spawn interactions between particles that break expected laws of nature. On the other side of the spectrum, there is a complimentary set of experiments that quietly observe their environments, patiently waiting to detect rare signals of dark matter and other new physical processes outside the realm of behavior described by the Standard Model. As the signals from the new physics are expected to be rare (~1 event per year as compared to the LHC’s billion events per second), the patient experiments must be exceedingly sensitive and avoid any imposter signals, or “background”, that would mimic or obscure the true signal.
The quest to decrease background interference has pushed experiments underground to cleanroom laboratories setup in mine caverns. While cleanrooms reduce the chances of unwanted radioactive isotopes, like radon-222, wandering into one’s experiment, mines provide a mile-thick shield from interference that would be present at the surface of Earth: particles called cosmic rays constantly pepper the Earth’s surface, but very few of them survive the long journey to an underground lab.
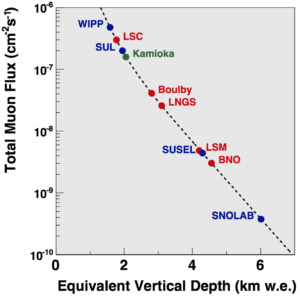
The form and function of modern underground experiments emerged from the collective insights and discoveries of the scientific community studying rare physical processes. As in any field of science, this community has progressed through decades of experimentation with results being communicated, critiqued, and validated. Scientific conferences have played an essential role in this process by bringing the community together to take stock of progress and share new ideas. The recent conference on Topics in Astroparticle and Underground Physics (TAUP) was a forum for scientists working to detect dark matter and study the properties of neutrinos. Suitably, the conference was held in the historic mining town of Sudbury, Ontario, home to the Creighton Mine, at the bottom of which lies SNOLAB, a world-class underground physics laboratory which notably housed the 2015 Nobel Prize winning SNO experiment. SNO, along with the Super-Kamiokande experiment in Japan’s Kamioka mine, was awarded “for the discovery of neutrino oscillations, which shows that neutrinos have mass.”
There is a natural excitement upon entering an active nickel mine, donning a set of coveralls, and catching a cage ride down into the depths; this was our entrance into the Creighton Mine during the TAUP conference. After descending an ear-popping 6800 feet in four minutes, we stepped out of the cage into tunnels— known as drifts— of raw rock. From there, we followed the path taken everyday by SNOLAB scientists, walking approximately one kilometer through the drifts to the SNOLAB campus. At SNOLAB, we prepared to enter the clean laboratory space by removing our coveralls, showering, and donning cleansuits. Inside, the rock walls are finished over with concrete and epoxy paint and we walked through well-lit hallways to a number of experiments which occupy impressively large caverns, some ~100 feet high.

Our tour of SNOLAB included visits to several dark matter experiments, including DEAP-3600 and MiniClean, which attempt to catch the faint glimmer of light produced by the potential interaction of dark matter particles with liquid argon. A stop by PICO-60 educated visitors on another captivating experiment, which monitors a volume of a super-heated chemical fluid for bubbles that would indicate the interaction of a dark matter particle and a nucleus. The tour also included the SNO+ experiment, offering glimpses of the search for a rare nuclear transformation of the isotope tellurium-130; because this transformation depends on the nature of neutrinos, its observation would further our understanding of these particles.
SNOLAB is also home to underground experiments from other fields. The HALO experiment, for instance, monitors the galaxy for supernovae by capturing neutrinos that are emitted by stellar explosions; neutrinos may provide the first warnings of supernovae as they are able to escape the confines of a dying star prior to any other species of particle. Additionally, the REPAIR experiment studies the DNA of fish kept underground, away from the natural levels of radiation experienced by all life on the surface of Earth.
The search for rare signals from new physical phenomena pushed physicists far underground and required the development of new technologies that have been adapted by other scientific disciplines. The SNOLAB facility, in particular, has played a key role in helping physics revise its best model of the universe, and it can be expected that similar underground facilities around the world will continue to help scientists of many stripes reveal new facets of the natural world.
Peer edited by JoEllen McBride and Tamara Vital.
Follow us on social media and never miss an article: