What do giraffes, angelfish, and seashells all have in common? Their surface patterns, from the patches on giraffe coats to the stripes on the angelfish, are formed through the reaction-diffusion process.
The reaction-diffusion process, or the Turing process, is a mathematical model describing how self-regulating patterns arise in organisms. Through the Turing process, an activator substance produces more of itself and also turns on an inhibitor substance. This inhibitor substance diffuses more quickly than the activator and turns off the activator. When the activator and inhibitor substances control coat pigments, periodic coat patterns, such as the giraffe’s patches are produced.
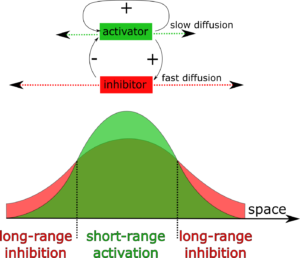
By varying factors, such as the diffusion speeds of the activator and inhibitor substances, mathematicians and biologists can predict different patterns ranging from spots to stripes that arise through this self-regulating process. If you’ve ever attended a social gathering, you’ve probably been part of a Turing process as people chat in small groups. Two people chatting often attract more people to join the conversation, but once the group gets large enough people will naturally split off and form a different group. If you looked at the room from an aerial view, you would see a spotted pattern.
Biologists now recognize that the Turing process can explain these fantastic patterns. However, this wasn’t always the case. Mathematician Alan Turing, probably better known for cracking the enigma machine in WWII, also dabbled in theoretical biology. He published this self-regulating pattern idea in 1952, shortly before his untimely death weeks before his 42nd birthday. For decades, biologists were skeptical of the plausibility of the Turing process, since it seemed unlikely that such a simple model could capture complex patterns and the lack of experimental evidence. However, 20 years later, mathematical biologists rediscovered the Turing process by reproducing animal skin patterns through computer simulations. Additionally, experimentalists observed how zebrafish stripe patterns change shape when pigment cells are removed from a developing fish. Through these types of experiments and simulations, the Turing process is now widely accepted by biologists.

The Turing process is commonly used to model eye-catching animal prints, but developmental biologists use the Turing process to understand embryology. Turing process simulations have predicted the number of mouse fingers formed to feather follicle development in chicks.
Recently, a study used the Turing process to model molar crown topography development of upper and lower molars in mice, since upper and lower molars are complementary to each. The scientists captured where peaks and valleys of the upper and lower molars form as the tooth grows using Turing process simulations. They found the upper and lower molars of mice resulted from a ‘striped’ or ‘spotted’ Turing processes respectively, just by assigning distinct factors to each type of molar, including how quickly the activator and inhibitor substances diffused and how fast the activator made more of itself, to switch from spots to stripes. Interestingly, these researchers also demonstrated that wildly different tooth topographical features found across different types of mammals can be produced just by adjusting a few of these parameters. This suggests that the teeth of different mammals such as vegetarians, omnivores, and carnivores might arise from varying a couple of factors across their evolutionary histories.
Considering the Turing process was only initially proposed less than a century ago, I can’t wait to see what other biological patterns can be described using the Turing process in the next century as further complexities are considered in the model.
Peer Editor: Hunter Hughes